| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 개발자
- 비동기
- csr
- 자바스크립트
- 프론트엔드
- Git
- http
- SSR
- 공부
- error
- html
- css
- 에러
- React
- dynamic import
- 코딩테스트
- Next.js
- React Query
- TypeScript
- 취업준비
- 알고리즘
- 취업
- 차이
- DOM
- Vite
- 백준
- JavaScript
- 코딩
- Browser
- Sass
- Today
- Total
minTech
[Algorithm] 이진 트리(Binary Tree)와 트리 순회(Tree Traversal) 본문
이진 트리
트리 구조는 하나의 루트로부터 여러 갈래로 뻗어나가는 구조를 말한다.
이진 트리라는 것은 아래 그림과 같이 트리 구조 중에서도 자식 노드가 최대 2개를 갖는 구조이다.
자식 노드가 최대 2개이기 때문에 왼쪽, 오른쪽으로 구분이 가능하다.

이진 트리의 종류
1. Full Binary Tree (정 이진 트리)
- 모든 노드의 자식노드가 2개 이거나, 아예 없다.
2. Complete Binary Tree (완전 이진 트리)
- 마지막 레벨을 제외한 모든 노드가 2개의 자식 노드를 가진다.
마지막 레벨의 노드는 최소 왼쪽이 다 채워져 있다.
3. Perfect Binary Tree (포화 이진 트리)
- 모든 노드의 자식 노드가 2개이며, leaf node의 레벨이 같다.



이진 트리 구현
이진 트리를 javascript를 통해 구현하는 방법에는 배열을 이용하는 방식과 연결 리스트를 이용하는 방식이 있다.
1. 배열을 이용하는 방식
배열을 이용해 구현하기 위해서는 아래 그림과 같이 각각의 노드에 인덱스를 부여한다.
인덱스의 순서는 위의 루트노드에서부터 아래로, 왼쪽부터 순서대로 부여한다.

부여하는 방식은 루트 노트의 인덱스를 0으로 잡고, 아래와 같이 자식노드의 인덱스를 구한다.
- 왼쪽 자식 노드의 인덱스 = 부모 노드 인덱스 * 2 + 1
- 오른쪽 자식 노드의 인덱스 = 부모 노드 인덱스 * 2 + 2

배열을 사용하여 구현하면 별다른 연산 없이 자식 노드에 빠르게 접근이 가능하고, 구현하기가 쉽다는 장점이 있어 완전 이진 트리를 구현하는데 굉장히 용이하다. 하지만 완전 이진 트리가 아닌 편향 이진 트리 같이 중간 중간 노드 들이 비어있는 노드의 경우에는 많은 공간이 낭비도리 수 있고, 배열 크기 이상의 노드를 추가할 수 없다는 단점을 갖는다.
2. 연결 리스트를 이용하는 방식
각각의 노드는 자신의 왼쪽, 오른쪽 자식 노드가 누구인지 알아야한다.
즉, 각 노드는 자신이 들고 있는 데이터, 왼쪽 자식 노드, 오른쪽 자식 노드에 대한 정보를 갖고 있게 되는 것이다.
따라서 노드와 루트 노드를 초기화하는 코드는 아래와 같이 작성할 수 있다.
// 노드 초기화
const Node = function(data) {
this.value = value;
this.left = null;
this.right = null;
}
// 루트 노드 초기화
const bTree = function(data) {
this.root = null
}
초기화한 노드를 통해 각각의 노드를 생성한다.
해당 메서드는 왼쪽 자식 노드와, 오른쪽 자식 노드, 자신의 데이터를 입력받아 노드에 연결한다.
bTree.prototype.makebTreeNode = function(left, right, data) {
const newNode = new Node(data);
newNode.left = left;
newNode.right = right;
this.root= = new Node;
}
이제 해당 메서드를 통해, 각각 왼쪽과 오른쪽, 노드의 데이터 값을 넣어주면서 트리를 완성한다.
연결 리스트로 이진 트리를 구현하면 필요없는 노드 생성을 하지 않기 때문에 메모리적으로 효율적이다.
트리 순회
트리의 모든 노드를 한 번식 방문하는 것을 트리 순회(Tree traversal) 라고 한다.
트리 순회 방법에는 깊이 우선 순회 방법(Depth First Traversal)과 너비 우선 순회 방법(Breadth First Traversal) 이 있고,
깊이 우선 순회 방법 중에서도 루트 노드를 언제 방문하냐에 따라 전위 순회(Pre-order traversal), 중위 순회(In-order traversal), 후위 순회(Post-order traversal)로 나뉜다.
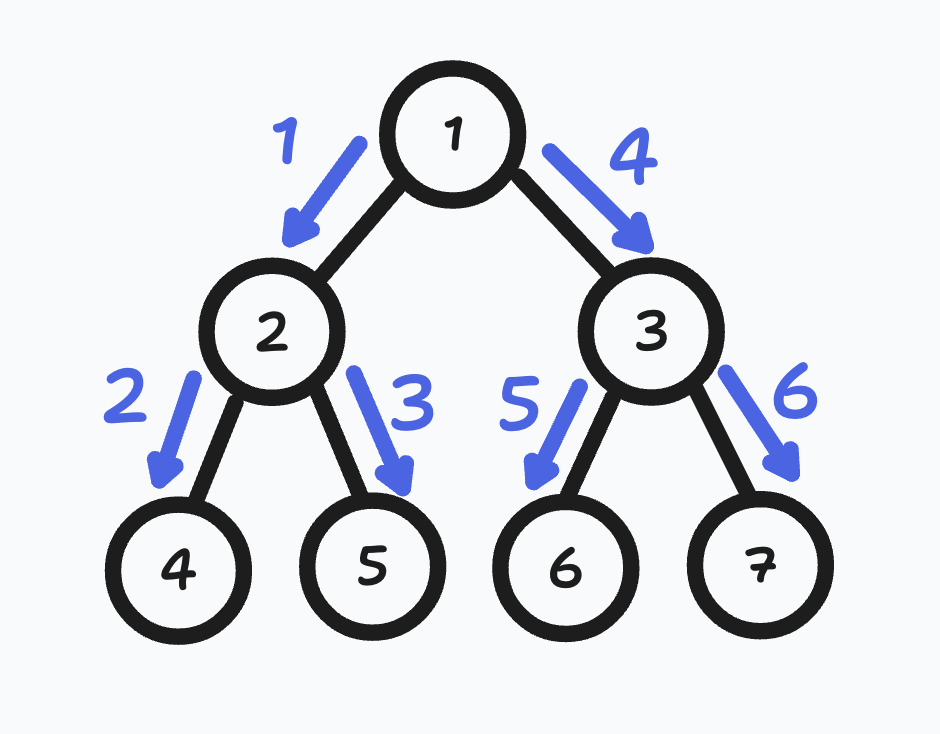
1. 전위 순회
- 루트 노드에서부터 시작한다.
- 루트로부터 왼쪽의 노드들을 순차적으로 방문한후, 왼쪽이 노트 탐색이 끝나면 오른쪽 노드를 탐색한다.
function preOrder (node) {
if(!node) return;
console.log(node.value);
this.preOrder(node.left);
this.preOrder(node.right);
}2. 중위 순회
- 루트 노드를 중간에 방문한다.
- 왼쪽 끝부터 순회를 시작한다.
- 왼쪽의 노드의 방문이 끝나면 루트를 거친 후 오른쪽으로 이동하여 탐색을 마무리한다.

function inOrder (node) {
if(!node) return;
this.inOrder(node.left);
console.log(this.value);
this.inOrder(node.right);
}
3. 후위 순회
- 왼쪽 끝부터 순회를 시작한다.
- 왼쪽 노드 방문이 끝나면 오른쪽으로 이동한 후, 루트를 방문하여 탐색을 마무리한다.

function postOrder (node) {
if(!node) return;
this.postOrder(node.left);
this.postOrder(node.right);
console.log(this.value);
}
📚 참고 자료
https://velog.io/@porupit0122/JavaScript-%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-4-%ED%8A%B8%EB%A6%AC
https://doheelab.github.io/algorithm/binary_tree/
'Algorithm' 카테고리의 다른 글
| [Algorithm] 백준 1074번 Z (Javascript, node.js) (0) | 2025.04.01 |
|---|---|
| [Algorithm] 플로이드 와샬 알고리즘 (1) | 2025.03.10 |
| [Algorithm] LCS(Longest Common Subsequence) (0) | 2025.01.14 |
| [Algorithm] Union-find 로 노드 고리를 찾아보자! (2) | 2024.12.13 |
| [Algorithm] Math.floor / Math.ceil / Math.round (0) | 2024.09.06 |




